Selecting the Number of Factors in Exploratory Factor Analysis via out-of-sample Prediction Errors
Exploratory Factor Analysis (EFA) identifies a number of latent factors that explain correlations between observed variables. A key issue in the application of EFA is the selection of an adequate number of factors. This is a non-trivial problem because more factors always improve the fit of the model. Most methods for selecting the number of factors fall into two categories: either they analyze the patterns of eigenvalues of the correlation matrix, such as parallel analysis; or they frame the selection of the number of factors as a model selection problem and use approaches such as likelihood ratio tests or information criteria.
In a recent paper we proposed a new method based on model selection. We use the connection between model-implied correlation matrices and standardized regression coefficients to do model selection based on out-of-sample prediction errors, as is common in the field of machine learning. We show in a simulation study that our method slightly outperforms other standard methods on average and is relatively robust across specifications of the true model. An implementation is available in the R-package fspe, which I present here with a short code example.
We use a dataset with 24 measurements of cognitive tasks from 301 individuals from Holzinger and Swineford (1939). Harman (1967) presents both a four- and five-factor solution for this dataset. In the four-factor solution, the fifth factor corresponding to the variables 20–24 is eliminated. For this reason, we exclude variables 20–24, which gives us an example dataset in which we would theoretically expect four factors. This reduced dataset is is included in the fspe-package:
library(fspe)
data(holzinger19)
dim(holzinger19)## [1] 301 19head(holzinger19)## t01_visperc t02_cubes t03_frmbord t04_lozenges t05_geninfo t06_paracomp
## 1 20 31 12 3 40 7
## 2 32 21 12 17 34 5
## 3 27 21 12 15 20 3
## 4 32 31 16 24 42 8
## 5 29 19 12 7 37 8
## 6 32 20 11 18 31 3
## t07_sentcomp t08_wordclas t09_wordmean t10_addition t11_code t12_countdot
## 1 23 22 9 78 74 115
## 2 12 22 9 87 84 125
## 3 7 12 3 75 49 78
## 4 18 21 17 69 65 106
## 5 16 25 18 85 63 126
## 6 12 25 6 100 92 133
## t13_sccaps t14_wordrecg t15_numbrecg t16_figrrecg t17_objnumb t18_numbfig
## 1 229 170 86 96 6 9
## 2 285 184 85 100 12 12
## 3 159 170 85 95 1 5
## 4 175 181 80 91 5 3
## 5 213 187 99 104 15 14
## 6 270 164 84 104 6 6
## t19_figword
## 1 16
## 2 10
## 3 6
## 4 10
## 5 14
## 6 14Next to providing the data to the fspe() function we specify that factor models with 1, 2, … ,10 factors should be considered (maxK = 10), that the cross-validation scheme should use with 10 folds (nfold = 10) and be repeated 10 times (rep = 10), and that prediction errors (method = "PE") should be used. An alternative method (method = "CovE") computes an out-of-sample estimation error on the covariance matrix instead of a prediction error on the raw data. This is a method that is similar to the one proposed by Browne & Cudeck (1989). Finally, we set a seed so that the analysis demonstrated here is fully reproducible.
set.seed(1)
fspe_out <- fspe(holzinger19,
maxK = 10,
nfold = 10,
rep = 10,
method = "PE",
pbar = FALSE)We can inspect the out-of-sample prediction error averaged across variables, folds, and repetitions as a function of the number of factors:
par(mar=c(4.5,4,0,1))
plot.new()
plot.window(xlim=c(1,10), ylim=c(0.6, 0.8))
axis(1, 1:10)
axis(2, las=2)
title(xlab="Number of Factors", ylab="Out-of-sample Prediction Error")
points(which.min(fspe_out$PEs), min(fspe_out$PEs), cex=3, col="red", lwd=2)
lines(fspe_out$PEs, lwd=2)
abline(h=min(fspe_out$PEs), col="grey", lty=2, lwd=2)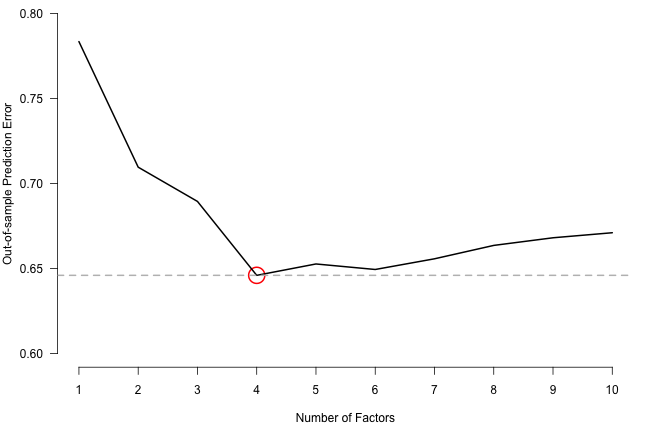 We see that the out-of-sample prediction error is minimized by the factor model with four factors. The number of factors with lowest prediction error can also be directly obtained from the output object:
We see that the out-of-sample prediction error is minimized by the factor model with four factors. The number of factors with lowest prediction error can also be directly obtained from the output object:
fspe_out$nfactor## [1] 4The un-aggregated of the 10 repetitions of the cross-validation scheme can be found in fspe_out$PE_array.
